The arithmetic [I] * 2.1 above hints at a larger truth.
Sketch operators work on scalars, vectors, points, and
transforms according to the general rules of affine algebra.
This can be helpful for setting up diagrams with computed geometry.
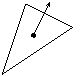
For example, if you have triangle vertices (p1) through
(p3) and need to draw a unit normal vector pointing out of
the center of the triangle, this code does the trick.
def p1 (1,0,0) def p2 (0,0.5,0) def p3 (-0.5,-1,2) def O (0,0,0) def N unit( ((p3) - (p2)) * ((p1) - (p2)) ) def n1 ((p1)-(O) + (p2)-(O) + (p3)-(O)) / 3 + (O) def n2 (n1)+[N] polygon(p1)(p2)(p3) line[arrows=*->](n1)(n2)The first line computes the cross product of two edge vectors of the triangle and scales it to unit length. The second computes the average of the vertices. Note that subtraction and addition of the origin effectively convert vectors to points and vice versa. The line command draws the normal at the correct spot.

Two caveats regarding this example remain. First, the only way to use
PSTricks-style arrows is with arrows=.
The alternative syntax for PSTricks arrows is not allowed in
sketch. Second, you might like to eliminate the third
def and write instead the following.
line[arrows=*->](n1) (n1)+[N]This is not allowed. The point lists in drawables may consist only of explicit points or point references. You may, however, use arithmetic to calculate point components. The following works, though it's a little cumbersome.
line[arrows=*->](n1)((n1)'x+(N)'x, (n1)'y+(N)'y, (n1)'z+(N)'z)Obviously, the tick operator 'x extracts components of points and vectors.