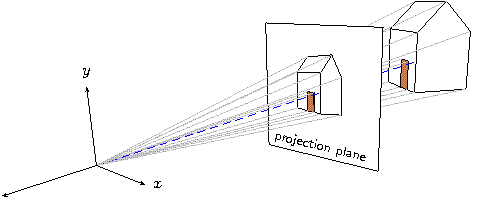
As an overview, let's develop a diagram that shows how a perspective
projection transform
works. We'll start with the traditional reference object
used in computer graphics textbooks, a house-shaped prism. Begin
by defining the points of the house. Rather than defining the faces
of the house as polygons and transforming those, we are going to
transform the points themselves with sketch arithmetic so that
we have names for the transformed points later.
% right side (outside to right) def R1 (1,1,1) def R2 (1,-1,1) def R3 (1,-1,-1) def R4 (1,1,-1) def R5 (1,1.5,0) % left side (outside to right--backward) def W [2,0,0] def L1 (R1)-[W] def L2 (R2)-[W] def L3 (R3)-[W] def L4 (R4)-[W] def L5 (R5)-[W]To add a door to the house, we use a polygon slightly in front of the foremost face of the house.
% door def e .01 def D1 (0,-1,1+e) def D2 (.5,-1,1+e) def D3 (.5,0,1+e) def D4 (0,0,1+e)Now let's create a new set of points that are a to-be-determined transform of the originals.
def hp scale(1) % house positioner def pR1 [[hp]]*(R1) def pR2 [[hp]]*(R2) def pR3 [[hp]]*(R3) def pR4 [[hp]]*(R4) def pR5 [[hp]]*(R5) def pL1 [[hp]]*(L1) def pL2 [[hp]]*(L2) def pL3 [[hp]]*(L3) def pL4 [[hp]]*(L4) def pL5 [[hp]]*(L5) def pD1 [[hp]]*(D1) def pD2 [[hp]]*(D2) def pD3 [[hp]]*(D3) def pD4 [[hp]]*(D4)Note the use of a transform definition and transform references. Now define the seven polygonal faces of the house and the door using the transformed points as vertices. Be careful with vertex order!
def rgt polygon (pR1)(pR2)(pR3)(pR4)(pR5)
def lft polygon (pL5)(pL4)(pL3)(pL2)(pL1)
def frt polygon (pR2)(pR1)(pL1)(pL2)
def bck polygon (pR4)(pR3)(pL3)(pL4)
def tfr polygon (pR1)(pR5)(pL5)(pL1)
def tbk polygon (pR5)(pR4)(pL4)(pL5)
def bot polygon (pR2)(pL2)(pL3)(pR3)
def door polygon[fillcolor=brown] (pD1)(pD2)(pD3)(pD4)
def house { {rgt}{lft}{frt}{bck}{tfr}{tbk}{bot}{door} }
Time for a sanity check. Add the line
{house}
and this is what we get.

This is correct, but does not reveal very much. Common errors are
misplaced vertices and polygons missing entirely due to incorrect
vertex order.
To rule these out, let's inspect all sides of the
house. This is not hard. Merely replace the reference
{house} with a repeat. See Repeats.
repeat { 13, rotate(30, [1,2,3]), translate([3,0,0]) } {house}

Again things look correct. Note that the hidden surface algorithm handles intersecting polygons correctly where some copies of the house overlap.
Let's lay out the geometry of perspective projection of the house onto a plane with rays passing through the origin. Begin by positioning the house twelve units back on the negative z-axis and adding a set of coordinate axes. To move the house we need only change the “house positioning” transform defined earlier.
def hp rotate(-40, [0,1,0]) then translate([0,0,-12])
def axes {
def sz 1
line [arrows=<->] (sz,0,0)(O)(0,sz,0)
line [arrows=->] (O)(0,0,sz)
line [linewidth=.2pt,linecolor=blue,linestyle=dashed] (O)(0,0,-10)
special |\uput[r]#1{$x$}\uput[u]#2{$y$}\uput[l]#3{$z$}|
(sz,0,0)(0,sz,0)(0,0,sz)
}
Time for another test. Let's build a real view transform,
creating a virtual camera
to look at the scene we are constructing. Replace the repeat
with
def eye (10,4,10)
def look_at (0,0,-5)
put { view((eye), (look_at)) } { {house}{axes} }
The view transform repositions the scene so that the point
eye is at the origin and the direction from eye to
look_at is the negative z-axis. This requires a
rotation and a translation that are all packed into the constructor
view.
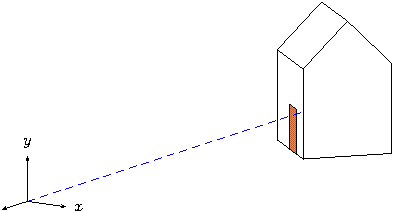
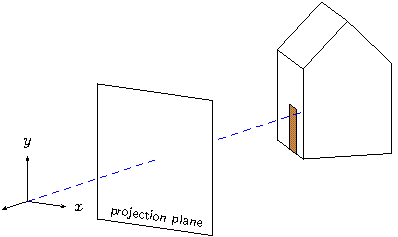
This is starting to look good! Add the projection plane half way
between the origin and the house at z=-5. We'll try
the angle argument feature of special to position a label.
def p 5 % projection distance (plane at z=-p)
def projection_plane {
def sz 1.5
polygon (-sz,-sz,-p)(sz,-sz,-p)(sz,sz,-p)(-sz,sz,-p)
special |\rput[b]#1-2#3{\footnotesize\sf projection plane}|
(-sz,-sz,-p)(sz,-sz,-p)(0,-sz+.1,-p)
}
Add {projection_plane} to the list of objects in the
put above.
The way we constructed the points of the house now makes it easy to draw rays of projection. We'll cast one ray from every visible vertex of the house and define options so the appearance of all rays can be changed at the same time.
def projection_rays {
def rayopt [linewidth=.3pt,linecolor=lightgray]
line [rayopt](O)(pR1) line [rayopt](O)(pR2) line[rayopt](O)(pR3)
line [rayopt](O)(pR4) line [rayopt](O)(pR5)
line [rayopt](O)(pL1) line [rayopt](O)(pL2) line[rayopt](O)(pL5)
line [rayopt](O)(pD1) line [rayopt](O)(pD2)
line [rayopt](O)(pD3) line [rayopt](O)(pD4)
}
The result is shown here.
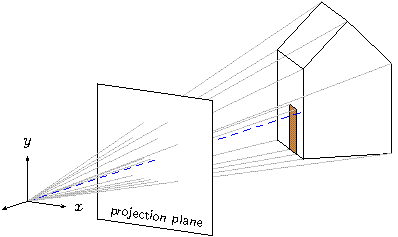
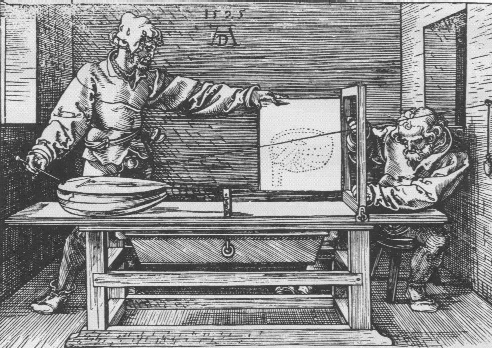
The rays pierce the projection plane at the corresponding points on the perspective image we are trying to draw. Albrecht Dürer and his Renaissance contemporaries had the same idea in the early 1500's.
All that's left is to find a way to connect the points of the house
on the projection plane. We could pull out a good computer graphics
text, find the necessary matrix, and enter it ourselves as a
transform literal. See Transform literals. That work is
already done, however. We can use the project(p) constructor.
There are still some details that require care. Projection will flatten whatever is transformed onto the plane z=-p. Therefore any part of the house could disappear behind the projection plane (the hidden surface algorithm orders objects at the same depth arbitrarily). The door may also disappear behind the front of the house. To make sure everything remains visible, we'll place the house a tiny bit in front of the projection plane and a second copy of the door in front of the house.
def projection {
% e is a small number defined above
put { project(p) then translate([0,0,1*e]) } {house}
put { project(p) then translate([0,0,2*e]) } {door}
}
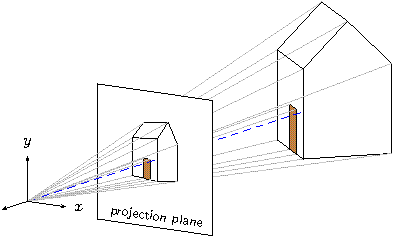
If you have studied and understand all this, you are well on the way
to success with sketch. Not shown are the 20 or so iterations
that were required to find a reasonable viewing angle and house
position, etc. Nonetheless, this drawing was completed in about an
hour. While a GUI tool may have been a little faster, it is unlikely
that a new drawing, itself a perspective projection of the scene,
could be generated with two more minutes' work! Just change the view
transform to
put { view((eye), (look_at)) then perspective(9) } { ...
and produce this.